Introducere
Distanța dintre două puncte poate fi definită ca lungimea liniei drepte care le unește. Această distanță este un concept fundamental în geometrie și este utilizată în multe aplicații practice, cum ar fi navigația, grafica computerizată și analiza de date.
Corpul principal
1. Sistem de coordonate
Pentru a înțelege formula distanței dintre două puncte, trebuie să înțelegem mai întâi conceptul de sistem de coordonate. Un sistem de coordonate este o modalitate de a atribui numere (coordonate) punctelor din spațiu. Cele mai comune sisteme de coordonate sunt sistemul de coordonate cartezian și sistemul de coordonate polare.
2. Formula distanței
Formula distanței dintre două puncte într-un sistem de coordonate cartezian este:
d = sqrt((x2 – x1)^2 + (y2 – y1)^2)
Această formulă se bazează pe teorema lui Pitagora, unde x1 și y1 reprezintă coordonatele primului punct, iar x2 și y2 reprezintă coordonatele celui de-al doilea punct.
3. Exemplu de aplicare
Pentru a ilustra cum funcționează formula distanței dintre două puncte, să presupunem că avem două puncte într-un sistem de coordonate cartezian: A(-2, 3) și B(4, -1). Putem utiliza formula distanței pentru a calcula distanța dintre aceste două puncte:
d = sqrt((4 – (-2))^2 + (-1 – 3)^2)
d = sqrt(6^2 + (-4)^2)
d = sqrt(36 + 16)
d = sqrt(52)
d ≈ 7.21
4. Sistem de coordonate polare
În afara sistemului de coordonate cartezian, există și sistemul de coordonate polare. Acesta utilizează unghiurile și distanțele radiale pentru a reprezenta punctele într-un plan. Formula distanței dintre două puncte într-un sistem de coordonate polare este:
d = sqrt(r1^2 + r2^2 – 2r1r2cos(θ2 – θ1))
Această formulă se bazează pe teorema cosinusului și implică coordonatele polare (r1, θ1) și (r2, θ2) pentru cele două puncte.
5. Aplicații practice
Formula distanței dintre două puncte are o gamă largă de aplicații practice. De exemplu, în navigație, aceasta poate fi utilizată pentru a calcula distanța dintre două coordonate GPS. În grafica computerizată, formula distanței este folosită pentru a determina cât de departe este un obiect de la un punct de vedere. În analiza de date, aceasta poate fi utilizată pentru a măsura similaritatea între două seturi de date.
6. Concluzie
Formula distanței dintre două puncte este o unealtă matematică esențială pentru a calcula distanța într-un sistem de coordonate. Este utilizată într-o varietate de domenii și are o gamă largă de aplicații practice. Înțelegerea acestei formule ne permite să rezolvăm diverse probleme și să obținem rezultate precise. Vă încurajez să încercați să aplicați această formulă în diferite contexte și să împărtășiți experiențele dvs. într-un comentariu.
Concluzie
Vă invit să lăsați un comentariu cu întrebări, sugestii sau exemple de aplicații practice ale formulei distanței dintre două puncte. Aștept cu nerăbdare să citesc părerile voastre și să discutăm mai multe despre acest subiect.
Formula Distantei Dintre 2 Puncte
Distanta Dintre 2 Puncte Distanta dintre doua puncte in plan cand se cunosc coordonatele … Distanţa între două puncte in plan. Fie un reper cartezian xOy formula distantei dintre doua puncte in plan este folosita pentru a calcula lungimea … sites.google.com Măsurați distanța dintre puncte – Comp – cv-inginer.ro
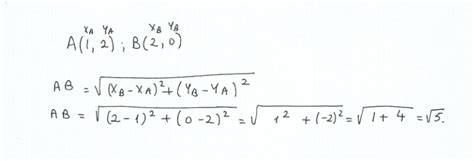
Puncte Coliniare Formula
Puncte Coliniare Ce inseamna puncte coliniare – Brainly.ro Punctele coliniare sunt punctele care apartin aceleasi drepte. De exemplu daca ai o dreapta AB si un punct M care se afla pe dreapta AB atunci A M … brainly.ro puncte coliniare Geometric vorbind avem o dreapta si pe ea avem doua puncte: A – cv-inginer.ro
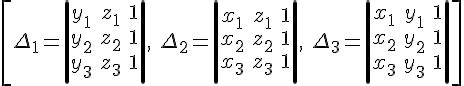
Formula Ecuatie De Gradul 2
Ecuatia de gradul 2 este una dintre cele mai importante concepte din matematică fiind folosită într-o varietate de domenii de la fizică și inginerie până la economie și chimie. Această ecuație este esențială pentru a găsi soluțiile pentru problemele care implică variabile ridicate la pătrat. În aces – cv-inginer.ro

Lasă un răspuns